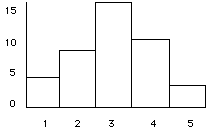Lab 11 Normal Distributions

Outline Normal distribution & areas under the curve Unit normal table for finding proportions of the curve
	Lab 11 Normal Distribution

Finding Probabilities in Distributions

We have already seen the f / N formula that we're now going to use. Think back to our frequency distribution tables. We used this formula to figure out proportions. In fact, probabilities are most often given as proportions (but you can also give them as fractions or percentages).

Consider the following frequency distribution table and its histogram.

___________________ X f_ p_ 5 2 .05 4 10 .25 3 16 .40 2 8 .20 1 4 .10
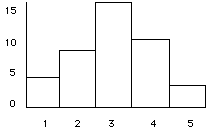histo

You can see that our proportion column corresponds to probability. It in turn corresponsd to the area under the curve (or in this case under the bars) for those intervals.

Imagine that they are numbered tokens in a bag, and that your task is to reach in and pull one out.

p (3) = f / N = 16 / 40 = .40

What is the probability of selecting (sampling) a 5?

What about more complex questions?

What is the probability of selecting a token with a value greater than 2?

p(X > 2) = ?
.05 + .25 + .40 = .70
histo

What is the probability of selecting a token with a value less than 5?

p(X < 5) = ? .10 + .20 + .40 + .25 = .95
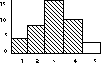histo

What is the probability of selecting a token with a value greater than 1 & less than 4?

p(4 > X > 1) = ? .20 + .40 = .60
histo

(1) Consider the following data. Draw a histogram of these data and answer the following questions.
a) What proportion of the scores is less than 4?
b) What proportion of the scores is greater than 4?
c) What proportion of the scores is greater than 1 and less than 4?
___________________
X	f_	p_    
5	5 	.10	
4	12	.24	
3	18	.36	
2	10	.20	
1	5	.10

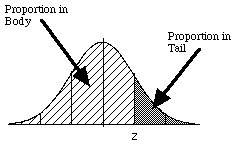
The Normal Distribution

One of the most commonly occuring distributions is the Normal Distribution.

Let's examine the Normal Distribution and see how we work with probabilities to find the area under the curve for different ranges of scores. If a distribution is normally distributed then it is symmetrical and unimodal. A graph of a normal distribution is shown below.

A few things to note about normal distributions:

Not all unimodal, symmetrical curves are normal, but a lot are.

For this class, we will not worry about how close a distribution is to normal, in fact for most of the course we'll assume that the distribution is normal.

The equation that defines a smooth curve like that above is referred to as a probability density function. In the case of the normal curve with a mean μ and a standard deviation σ, the probability density function is: $f (X) = 1 σ 2 π ‾ ‾ ‾ \sqrt e - 1 2 (X - μ σ) 2$

The area under the normal curve (or any other curve) must sum to 1. Why? remember that the area under the curve refers to the probabilities (or proportions) and the total probability must equal 1.

The normal distribution is often transformed into z-scores.

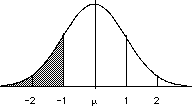
In the image below, you can see the proportions between each standard deviation interval.

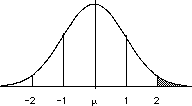
In the normal distribution with mean μ and a standard deviation σ:

34.13% of the scores will fall between the mean μ and 1 σ.

13.59% of the scores will fall between 1 σ & 2 σ.

2.28% of the scores will fall between the 2 σ & 3 σ.

This relationship is sometimes referred to as the "68-95-99.7 Rule".

In the normal distribution with mean μ and standard deviation σ

68% of the observations fall within 1 σ of μ

95% of the observations fall within 2 σ of μ

99.7% of the observations fall within 3 σ of μ

normal

Answer the following questions about the normal distribution:
(2a) What percentage of the area under the curve is between the mean and the right most end of the curve?
(2b) What percentage of the area under the curve is within one standard deviation of the mean (on either side)?

Using z-scores with Normal Distributions

An important tool that we'll use is the unit normal table. You'll find it in the back of your reading packet. In this table are a bunch of z-scores and proportions for the Standard Normal Distribution (which is the z-score standarized Normal distribution). In other words this table allows you to figure out the area under the curve (and thus the probability of sampling) at nearly every position on the curve (defined in z-scores). One thing to keep in mind about this table is that is that there are several ways that it gets organized, depending on the source. So make sure that you understand the Unit Normal Table that you are using.

Using the unit normal table.

z	.00	.01
-3.4 -3.3 : : 0.0 : : 1.0 : : 3.3 3.4	0.0003 0.0005 : : 0.5000 : : 0.8413 : : 0.9995 0.9997	0.0003 0.0005 : : 0.5040 : : 0.8438 : : 0.9995 0.9997

So by using the table, we can an ask about different areas under the curve. We can also go in both directions. That is, from the table of z-scores to probabilities and/or from probabilities to z-scores.

(3a) Find the probabilities that correspond to the area to the right of the following z-scores: 2.0, 0.5, -0.75, -2.0 (hint: sketch the distribution and locate the score).
(3b) Find the z-scores that correspond to the following probabilities: 0.5000, 0.8413, 0.3050 these probabilities correspond to areas to the right of the z-score (hint: a sketch will be helpful again)

What follows are procedures and examples of using the Unit Normal Table

Finding probabilities from z-scores

Finding z-scores from probabilities

Finding Percentile ranks

Note: Don't underestimate the value of drawing a picture of the distribution and trying to just "eyeball" the answer (in addition to doing the math). It just may save you from making a mistake.

Here is the "best" way to find a probability from the table:

step 1: sktech the distribution, showing the mean & standard deviation
step 2: sketch the score in question, being sure to place it on the correct side of the mean & roughly the correct distance from the mean
step 3: read the problem again to see if you need the probability of getting a score > or <. Shade this area on your sketch.
step 4: translate the X score into a Z-score
step 5: Use the correct column (and sign) to find the probability in the unit normal table.

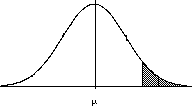
Let's look an an example like this:

Example:

Suppose we have a normal distribution of IQ scores with mean = 100 and sd = 15.

What is the probability of having an IQ of 85 or less?
p(X < 85)?

For IQ scores, μ = 100, σ = 15,
$z = I Q - μ σ = 85 - 100 15 = - 1$
Thus, 85 is −1 standard deviations below the mean.

--using the unit normal table:
z(-1) --> p = 0.1587

Now let's look at finding the z score if we know the probability. In this case we start with a probability and find the z score in the table. Once we have the z score we can use the z-score formula to solve for X to get the score.

Here is the "best" way to find a Z-score from a probability:

step 1: Sketch the normal distribution
step 2: shade the region corresponding to the required probability
step 3: locate the probability in the correct column of the table
step 4: label the edge of the shaded region with the z-score from the step above
step 5: compute the corresponding raw score (X).

** keep in mind that the percentile rank is equal to the probability of being at or below a given score. Thus, percentile ranks less than 50% refer to the lower tail.

Let's look an an example like this:

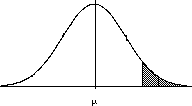
Example:

What IQ score do you need to have to be in the top 5% of the population?
The upper-tail is needed.
p = 0.05
---- look at the table --->
z = 1.65
so X = (1.65)(15) + 100 = 124.75

Sometimes we need to find the probability that X will fall between two scores rather than simply above a score or below a score.

step 1: Sketch the curve & shade the region of interest
step 2: Translate both scores to Z-scores
step 3: Look up the probabilities of scoring < or > each of the two z-scores
step 4: Add (or subtract) the probabilities accordingly

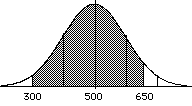
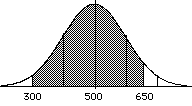
Example:
What is the prob. of scoring between 300 and 650 on the SAT?
recall: μ = 500, σ =100
p(z <  (650 - 500) = p(z < 1.5) = 0.9332
          100

p(z <  (300 - 500) = p(z < -2.0) = 0.0228
          100
the .9332 from 650 includes the lower tail, so we determine the proportion in the lower tail, and subtract that p(300 < z < 650) = .9332 - .0228 =.9104
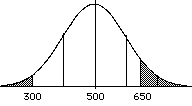
You might want to know what percentage lies outside two points (essentially the opposite of the last situation).

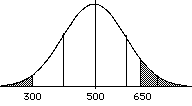
Example:
What is the prob. of scoring lower than 300 or higher than 650 on the SAT?
recall: μ = 500, σ =100
p(z >  (650 - 500) = p(z >  1.5) = 0.0668
          100

p(z < (300 - 500) = p(z <  -2.0) = 0.0228
          100
the two numbers both reflect the proportions in the tails, so we just need to add them together p(300 < z < 650) = .0668 + .0228 =.0896
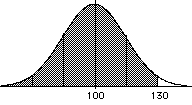
Another thing that you can use the unit normal table for is to find percentile ranks

Example:

What is your percentile rank if you have an IQ of 130?
for IQ scores μ = 100, σ =15
z = (130 - 100)/15 = 2.0
--look at the table--> p = 0.9772 --> percntile rank 97.72

Asking questions about the probability of getting a single score from the population.

Examples:

What is the probability of having an IQ of 130 or above?
p(X > 130)?

for IQ scores μ = 100, σ =15
z = (130 - 100)/15 = 2.0
--look at the table--> p = 0.0228

What is the probability of having an IQ of 85 or less?
p(X < 85)?

for IQ scores μ = 100, s =15,
z = (85 - 100)/15 = -1.0
--look at the table--> p = 0.1587

What IQ score do you need to have to be in the top 5% of the population?

The upper-tail is needed.
p = 0.05
---- look at the table --->
z = 1.65
so X = (1.65)(15) + 100 = 124.75

Finding out what the probability of a single score being within a range of scores in the population.

Example:
Suppose we have a normal distribution of SAT scores with μ = 500 and σ = 100.

What is the prob. of scoring between 300 and 650 on the SAT?

recall: μ = 500, σ =100
p(z <  (650 - 500) = p(z < 1.5) = 0.9332
          100

p(z <  (300 - 500) = p(z < -2.0) = 0.0228
          100
the .9332 from 650 includes the lower tail, so we determine the proportion in the lower tail, and subtract that p(300 < z < 650) = .9332 - .0228 =.9104
And finally, you might want to know what percentage lies outside two points (essentially the opposite of the last situation).

Example:
What is the prob. of scoring lower than 300 or higher than 650 on the SAT?
recall: μ = 500, σ =100
p(z >  (650 - 500) = p(z >  1.5) = 0.0668
          100

p(z < (300 - 500) = p(z <  -2.0) = 0.0228
          100
the two numbers both reflect the proportions in the tails, so we just need to add them together p(300 < z < 650) = .0668 + .0228 =.0896
(4) Now try some on your own:

(a) What is the probability of having an IQ of 130 or above?
(b) What is the probability of having an IQ of 120 or above?
(c) What is the probability of having an IQ score of 91 or less?

5) The scale for the SAT is set so that the distribution of scores is approximately normal with mean = 500 and standard deviation = 100. You think that you might need a tutor. You know of a tutoring service for students who score between 350 and 650 on the SAT. You think that you probably fit within their range. What is the probability that you will get an SAT score between 350 and 650?

6) The National Collegiate Athletic Association (NCAA) requires Division I athletes to score at least 820 on the combined mathematics and verbal parts of the SAT exam in order to compete in their first college year. In 1999, the scores of the millions of students taking the SATs were approximately normal with a mean = 1017 and a standard deviation = 209. What is the probability of scoring an 820 or less?

The Area Under the Normal Curve Spreadsheet

There are a variety of alternatives to looking things up in the unit normal table. For example, I've got an app on my iPhone called "Bell Curve." that provides an easy visual interface to get these values. Dr. Joel Schneider has developed an Excel spreadsheet tool to do this as well. If you are interested you can download this Excel spreadsheet tool and use it. Whatever method you use, I strongly suggest that you compare your answers with what you find in the table at first to make sure that you are using the method correctly.

To use this spreadsheet:

Select Score to Proportion if you know the score(s) and wish to calculate proportions or probabilities. Select Proportion to Score if you wish to know a raw score when you already know the probability or proportion.
Select Less Than, More Than, Between, or Exclude Between, depending on what you wish to do.
Enter the mean in the dark box at the top left.
Enter the standard deviation in the dark box at the top right.
Enter the raw score(s) or proportion(s) that are known in the dark boxes below the mean and standard deviation boxes. Remember that proportions MUST range from 0 to 1. Any value outside this range will result in an error.

Here is a silent demonstration of how to use the file:

Example:

Suppose you wish to know what proportion of scores are less than 5 when μ = 10 and σ = 3.

You know the score (i.e., 5) and you want to know a proportion so you select Score to Proportion.
You want to know how much of the scores are less than 5 so select Less Than.
Enter 10 as the mean
Enter 3 as the standard deviation.
Enter 5 as the raw score.

You should now see the answer (0.05) in the Proportion Under Curve box.

Outline

Lab 11

Normal Distribution

Finding Probabilities in Distributions

The Normal Distribution

Using z-scores with Normal Distributions

The Area Under the Normal Curve Spreadsheet

Example: