Outline

• Correlations
  • by-hand
  • Using SPSS procedures

So far we have spent most of our time looking at how a single variable is distributed. All the statistics we have studied are univariate statistics. However, as researchers, we are often more interested in how different variables may be related to one another. To investigate, we need bivariate statistics. In this lab we will examine ways in which we can describe how two variables (distributions of the variables) are related to one another. For this lab we will focus on describing this relationship as a descriptive statistic. In a later lab we will return to this issue, but as an inferential statistic (within the hypothesis testing framework).

Let's consider an example: suppose that we're interested in variables are related to a person's height (interval-ratio data so we're looking at the Pearson r test). Our first step is to identify a variable that we think might be related (e.g., teenagers height and the average of their parents' height), and then we examine how the distributions of each of these variables co-vary with one another. By co-vary, I mean, as the values of height go up, what happens with the corresponding values (your parent's average height)?

As we have already learned, Variance (the square of standard deviation) measures how much the values of a variable deviate from the mean. Covariance measures how much a pair of random variables tend to deviate in the same direction. For example, if we expect that a teenager's height and their parents average height are positively related, we should expect to see that teens who score high above the mean on height should also be likely to have parents taller than average. Teens who are shorter than average should have parents who are shorter than average.

We're going to look at several aspects of examining these relationships:

• Starting with graphical displays (scatterplots)
• Then we'll look at the statistical test (the Pearon r correlation coefficient)
• We'll then use the test in our hypothesis testing procedure
• And, last, we'll look at how SPSS calculates the Pearson r and creates scatterplots

Scatterplots

A scatterplot shows the relationship between two quantitative variables measured on the same individuals.

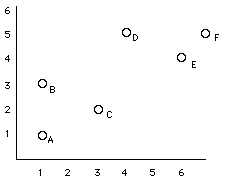
The values of one variable appear on one axis and the values of the other on the other axis. A point on the scatter plot represent the values of each variable for a particular individual. Note: if you have an experiment in which you've declared a response variable and an explanatory variable, always plot the response variable (Y) on the vertical axis and the explanatory variable (X) on the horizontal axis.

Consider the follwing example:

Data Set		Scatterplot
Person X Y A 1 1 B 1 3 C 3 2 D 4 5 E 6 4 F 7 5	Y
		X

Notice that each dot represents a single individual. The location of the dot is determined by the values of the two variables for that individual.

To interpret a scatterplot we should:

• Look for any overall pattern and for any striking deviations from that pattern.
• We can describe the overall pattern of a scatterplot by the form, direction, and strength of the relationship (we'll do this both by looking at the graph and then supplimenting it with numbers).

Form refers to how the scores cluster together.


• A linear relationship is one that can be described as more or less following a straight line. Correlations describe the strength of linear relationships only.  (most of our discussion will focus on linear relationships)
  
• A non-linear relationship is one in which there is a clear relationship but it does not follow a straight line. Examples of non-linear relationships are parabolas, ellipses, logarithms, trigonometric functions, and hyperbolas. This course will not discuss non-linear relationships other than to note that they exist. Correlations do not measure the strength of non-linear relationships.

Direction refers to the kind of relationship.


positively associated variables are when above-average values of one variable tend to accompany above average values of the other variable (and the same for below-average scores)
negatively associated variables are when above-average values of one variable tend to accompany below-average values of the other variable
no association when there doesn't appear to be a pattern to the scatterplot

Strength refers to the how tightly clustered the points are.

• In a strong relationship, the points are close to the best-fitting line. A perfect linear relationship is when all the points fall on a single line.
• In a weak relationship, the points are far from the best-fitting line.

As the figure below changes (note: it sometimes takes a while to load the animated picture), note how the strength changes as a function of how close or far the points are from the line.  If you watch long enough, you'll also see both positive and negative relationships depicted.

In the above example, we have a fairly linear relationship, the association is positive, and the points are fairly tightly clustered without any outliers.



(1) Match the following graphs to the descriptions:

A	B	C	D	E

_____ Strong negative association

_____ Strong positive association

_____ Medium strength negative association

_____ Medium strength positive association

_____ No association

Computing the Correlation Coefficient (r) (by hand)

Parts 1 and 2: Variability of X and Y separately: We'll use the Sum of Squares as a measure of variability for X and for Y (that is SS_X for variable X and SS_Y for variable Y).

SS_X is the sum of the squared deviations of each X from the mean of the X's.

SS_Y is the sum of the squared deviations of each Y from the mean of the Y's.

Part 3: Covariability of X and Y: We'll call this the Sum of the Products (SP)

What this means is that for each individual (each point on the scatter plot) we figure out how much X varies and how much Y varies. Then we multiply each of these deviations together. This gives us a measure of how much X and Y are varying together (or how much they covary).

So now we have the top and bottom parts of the equation, except for one detail. The scores in the denominator are squared deviations, so we need to take the square root of these. This leaves us the following formula:

This is the formula for the Pearson Correlation Coefficient. It is symbolized with the letter r when referring to a sample statistic and the Greek letter rho (ρ) when referring to a population parameter.

Another formula for the correlation coefficient is:

where s_xy is the sample covariance of X and Y and s_x and s_y are the sample standard deviations of X and Y, respectively. This formula can be derived from the previous formula by dividing both the numerator and the demonimator by 1/(n-1).

Okay, let's consider the following set of data:

Our first step should be to make the scatterplot, but to save time we will skip this step.

Our second step is to compute the correlation coefficient r. We'll start by computing the SP.

2) Make a table that looks like the one below and complete the missing blanks (feel free to use a calculator). 

	X	Y
	0	1
	10	3
	4	1
	8	2
	8	3
Sums	30	10
Means	6	2

Correlation and Scatterplots in SPSS

Open the dataset: height.sav This fictional dataset contains the height, weight, age, and gender information for 40 individuals.  Additionally, it has the average calcium intake, household income, and average parental height. 

Suppose that we want to examine the relationship between the age and income variables. 

In the menu, click Analyze → Correlate → Bivariate

Select the variables that you want correlated (you can have more than two at a time) and click the arrow button.

When you click OK, you will see the correlation matrix in the output window. The correlation between age and income (r = 0.328) is circled in red.

Now drag the variable you want on the horizontal axis onto the box that says X-axis. Drag the variable you want on the vertical axis onto the box that says Y-axis. For correlation, it doesn't make any difference what variables are entered on the X-Axis and Y-Axis.  For now, try plotting income as your Y variable and age as your X variable.  (We'll see later that if one variable is the explanatory variable, it goes on the X-axis, and the outcome variable goes on the Y-axis.)

Click OK and you will see a scatter plot like the one below.

Your instructions for the first correlation will look like this. To do successive correlations, you just have to drag-and-drop the different variables.

(3) Make scatterplots that plot the relationship between our response variable "height" and our 3 quantitative explanatory variables. (avgphgt, calcium, income). Cut and paste these into your worksheet. For each scatterplot describe the nature of the relationship (in terms of direction and strength).

(4) Make a scatterplot of height and weight and include gender as a categorical variable. (mark the cases by gender). Paste your scatterplot into your worksheet. How does the relationship between height and weight compare for men and women?

(5) Compute a correlation matrix that computes the correlation coefficients between 5 of our variables. (height, weight, income, calcium, avgphgt).  Copy and paste these into your worksheet.  Which variables have the strongest correlations?  Which variables are negatively correlated?