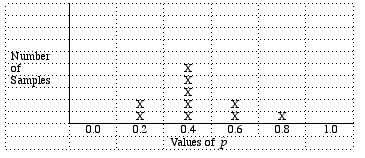Outline

  • randomness
  • basic probability
  • samples versus populations
  • simple random sampling
  • sampling error: variablility and bias
banner

Lab 5: Sampling & Basic Probability

Why and how we use samples

Most of our research questions are concerned with large groups of individuals. However, it is usually the case that we can't test all of these individuals (usually because of resouce limitations like not enough time and/or money). So, while we're interested in looking at the large group as a whole (our population) we typically only look at a subset of individuals (our sample). A result of using samples is that the interpretation of analyses that we make about populations is grounded in probability.

Today's lab focuses on some of the basic differences between populations and samples, and the impact of these differences on our research questions. We will start with a bit of discussion about samples and populations, then discuss some basic probability theory, and then bring these two topics together.

Populations and Samples

Let's begin by looking at a picture of a population.

Let's assume that each circle is an individual, and that all of the individuals together constitute our population. To protect their identities, each individual is identified by a number (00 - 99) rather than their actual name. The shaded circles are individuals that support a leagalization of gambling proposal, while the unshaded circles are those indviduals who do not support the proposal.

Suppose that our local congressperson wants to know how the population feels about the proposal. One way to go about this is to ask all 100 individuals what their view is. Go ahead and count up how many people support the proposal. To find the proportion of individuals who support the proposal, divide the number of individuals supporting the position by the total number of individuals in the population.

1) One way to go about this is to ask all 100 individuals what their view is. Go ahead and count up how many people support the proposal. Enter this answer on your Lab Worksheet. To find the proportion of individuals who support the proposal, divide the number of individuals supporting the position by the total number of individuals in the population

    proportion = p = 

      number of individuals supporting the position  
the total number of individuals in the population

Now let's suppose that, the congress person needed to know the answer that afternoon, and didn't have enough staff to locate and contact all of the indivuals in time. So instead, the Statistical Advisor to Congress (I don't think that such a position actually exists, but perhaps one should) suggests that sampling techniques should be used. That is, rather than contact all of the individuals in the population, the staff should contact a subset of the individuals (take a sample from the population). Let's consider some different possible samples.

A simple random sample - the staff selects some number of individuals (n) at random, and contacts those ten and asks for their opinion.

To the right is one such sample of ten individuals (n = 10)

Now remember the original question, what proportion of the individuals in the population support the proposal. How do we use the sample to answer this question?
We use the proportion from the sample as an estimate of the population proportion.
The formula is pretty much the same, except now instead of a p we use a phat (pronounced "p-hat"). The "hat" means that it is an estimated proportion.
phat= # of individuals in sample supporting the position
     the total # of individuals in the sample

So for this sample phat = 4/10 = .40

sample1

 

There are many different possible samples of n = 10. Consider the two more below.
sample2 sample 3

Notice that the three samples we just considered have different estimates of the population proportion.  When the sample proportion estimate is different from the population proportion we call this sampling error.  Notice too, that not every sample has the same amount of smapling error; so there is variability in how much error we have.  At first glance this seems like a BIG problem: How do we know which sample gives us the best estimate of the population proportion? Luckily for us (and the congressperson) there are statistical procedures to help with the problem.

Bring up the picture of a population again.

2) Using the population picture above (go back up and click the population button again), randomly select a sample of 5 individuals (choose 5 circles randomly). Compute the phat. Now do the same for 9 more samples of size n = 5. Type in all of these estimated proportions into your worksheet.

On your worksheet you'll see the axes for a graph, using X's plot your estimated proportions from your 10 samples on the graph.  While the proportions in your samples vary (and thus the sampling error), you may begin to notice a pattern.  What is the most common proportion among your 10 samples?


To the right is an example of what your graph for your samples might look like. 		graph

    3) Now let's repeat the process, taking 10 more samples and plotting them on your graph.  As we add more samples, a pattern should start to emerge.  What do you notice about the pattern of proportions as we add more and more samples?  (If you aren't sure, ask one of your lab neighbors to if you can add their samples to your graph and double your number to 40 samples)

Biased sampling

Suppose that the congressperson's staff decided not to do random sampling, but instead decided to just call individuals from the same area code (trying to save money on those long distance charges). This sampling method is an example of convenience sampling (selecting the individuals of the population that are easiest to reach). So let's reconsider our population of individuals along with an overlaid area code map.

Suppose that the congressional offices are located in the 217 area code. Samples taken from this sub-part of the population will typically have a higher estimation of the population proportion than the samples drawn using random sampling.

    4) Go ahead and select 5 samples of size n = 5 from this area code. Compute their estimated population proportions.

Stop and consider why the estimates are consistently different from those that we got from the random sample.

The reason is that these convenience samples are biased. Bias is a systematic difference between the population parameter (in this case the proportion of those agreeing with the proposal) and the sample estimates (called statistics) resulting from your method of sampling. This is different from the variability that we saw earlier, because the variability comes from random differences, while bias comes from the systematic (or consistent) differences.

    5) Suppose that the congressional offices are in the 204 area code. Would samples drawn from that area code have the same or different bias (or no bias) as those from the 217 area code? Why?

Convenience samples are typically biased even if the researcher doesn't know how. Bias is a systematic difference between the population parameter (in this case the proportion of those agreeing with the proposal) and the sample estimates (called statistics) that results from your method of sampling. This is different from the variability that we saw earlier, because the variability comes from random differences, while bias comes from the systematic (or consistent) differences.

Random events

What the above exercise is an attempt to show is that, while random events are somewhat unpredicatable in the short term (e.g., if you only take one or two samples, but that in the long term, across many repeated samples, random events usually have regular and predicatable pattern.

Random (chance) behavior is unpredictable in the short term, but has a regular and predictable pattern in the long run.

The probability of any outcome of a random phenomenon is a number between 0 and 1 that describes the proportion of times the outcome would occur in a very long series of repetitions.

This is why gambling casinos do so well.  While, the casino operators can't know how particular rolls of the dice, or hands of cards will be dealt, they do know the odds of dice rolls and cards hands based on long term outcomes.  So they set their payouts based on these odds and, over the long term, make their profits. 

How is this relevant to our statistics course?  The logic of inferential statistics is to estimate the probability of getting particular outcomes and make decisions based on these probabilities.  Why do we need to estimate probabilities?  Largely because we make observations on samples but want to make/test claims about populations.  Inferential statistical procedures are used to estimate the amount of sampling error in our samples and uses it to determine the probability that our results are due to random chance.  Later in the course we will go through the logical steps in this process.  For now we will start by discussing the basics of probability.



Basic probability

    We deal with probabilities everyday.

      - lotto tickets, weather forcasts, medical reports on the news (e.g., risks of cancer)

      In a situation where several different outcomes are possible, we define the probability for any particular outcome as a fraction or proportion. If the possible outcomes are identified as A, B, C, D, and so on, then:


      Probability of A = number of outcomes classified as A
      total number of possible outcomes

      The total number of possible outcomes (the bottom part of the equation) is called the sample space S

      Some Rules of probability

      • Any probability is a number between 0 and 1.0 (some people find it easier to think in terms of percentages, so 0 to 100%)
      • All possible outcomes together must have a probability equal to 1.0 (again, all possible outcomes add together to make 100% of the outcomes)
      • The probability that an event does not occur is 1 minus the probability that it does occur. (so if there is a 20% chance of something happening, then there is a 80% chance that it doesn't happen)
      • If two events have no common outcomes, then the probability that one OR the other occurs is the sum of their individual probabililties. (so if you roll a four-sided die, there is a 25% chance of getting each outcome 1,2,3, or 4.  The chances of getting a 1 or a 4 is 25% (for a 1) plus 25% (for a 4) = 50% chance).
        • 4sided-die
      • The probably of two independent outcomes both happening (A AND B) is the product of their two probabilities.  p(A) * p(B).  (using our 4-sided die example again.  If we rolled the die twice, what is the probability of first rolling a 1 AND then rolling a 4?  25% (rolling a 1) times 25% (rolling a 4) = 6.25%)


      Consider a concrete example:

        You are playing War (the card game) with your kid sister, each of you has your own deck of 52 cards. She picks the Queen of hearts from her deck. What are the odds that you'll pick the Queen of hearts from your deck? card

        There are 52 different cards in a deck, so the sample space is 52. There is only one queen of hearts. So: 

         prob of Q-hearts =  ____picking the Queen of hearts ___
		    total number of possible cards picked

        
= 1/ 52

      Notationally we can express this probability as: p(Q♥) = f / N = .019
          f = the frequency of queen of hearts in a standard deck of cards
          N = the total number of possible cards picked

      Now let you try a few.

        6) What is the probability of selecting a red card from a standard deck of playing cards (remember that there are two red suits: ♥ and ♦)?

        7) What is the probability of selecting a club (♣) from a standard deck of playing cards?

        8) What is the probability of selecting a club  (♣) or a heart (♥) from a standard deck of playing cards?

        9) What is the probability of selecting a 7♣ or 7♥ from a standard deck of cards?

        10) In each of the following situations, describe the sample space (i.e., possible outcomes) for the random phenomenon.

          a) A seed is planted in the ground. It either germinates or fails to grow.
          b) A patient with a usually fatal form of cancer is given a new treatment. The response variable is the length of time that the patient lives after treatment.
          c) A student enrolls in a statistics course and at the end of the semester receives a letter grade.
          d) A basketball player shoots four free throws. You record the sequence of hits and misses.
          e) A basketball player shoots four free throws. You record the number of baskets she makes.
            Note: (d) and (e) are different! In one case the are taking the "sequence" into account. Think about how that changes the question.  Hint: the sequence takes the order into account, but the number of baskets does not. So the sequence Hit-Miss (made the first, missed the second) is different than Miss-Hit (missed the first, hit the second).  But if we were just counting the hunber of made baskets, they'd both be the same (1 Hit).



Probability and Samples

    In the final section of our lab we will start bringing sampling and probability together (we will do this in greater detail in later labs).

    Imagine the following situation.  You are Jack and you are on the way to town to sell your cow. You are approached by a stranger who claims to have "magic" beans. He produces a bag, and pours out 10 beans, 2 are white and 8 are black.  jack
    The black beans, he says, are magic, but the white are not. He places the beans back into the bag and places it into his pocket. He then offers to buy your cow for his bag of beans. However, you a somewhat suspicious when he pulls the bag back out of his pocket. You ask to see the beans again, but he refuses. He claims that if he removes the beans too often the beans black beans will lose their magic, changing color from black to white. You say "Well, how do I know that's the same bag you showed me?" He agrees to allow you to remove four beans from the bag. You agree and he pours out four beans, 1 is white, the others are black. Do you, as Jack, think that the bag is the original bag with 2 white and 8 black beans?

    Let's bring the story back to our statistical discussion. We can consider the original bag of beans our population and the two beans that he showed us from the current bag our sample. Our question here is, looking at the sample can we know for certain whether the current bag is the original bag or not? Because we can't see the contents of the entire bag, we can't know for sure. However, we can take into account the probability of getting particular samples.

    In the situation described in the story, the population bag had 80% black "magic" beans (8 out of 10). The sample of 4 beans had 75% black beans. 75% is pretty close to 80%. The likelihood of selecting this sample from the original population is fairly high. So Jack will probably conclude that the current bag is the same as the original bag. jack However, suppose that when the stranger had poured out a different sample of 4 beans. What would you have concluded if the sample had consisted of 2 white and 2 black beans? Here there is a larger difference between the proportion of black to white beans in the sample and the original population. This sample is still possible, however it is less likely than the earlier sample. So in this situation, Jack may be more likely to think that the current bag is not the original bag and that the stranger is trying to pull a fast one.  What if the sample had 3 white and 1 black.  Then Jack would know for sure that the bags had been switched (the original back only had 2 white beans, so a sample from it can't have 3).

    This is the kind of situation that a researcher is often in, trying to look at a sample of observations and make a decision about what population the sample came from. For now, we're just trying to get this at an intuitive level, but later in the course (especially aroung lab 15) we will learn how to quantify the probabilities used to make these kinds of decisions.

      11) Consider the following populations and samples.  For each try to decide which population the sample was more likely to have been drawn from.

      a)  A standard deck (population 1) has 52 cards, one copy of Duece (2) through Ace for each of the four suits ( ♥, ♦, ♣, ♠); a Pinochle deck (population 2) has 48 cards, two from each of the four suits, 9 through Ace (9,10,J,Q,K,A).  If you were dealt 9♥, 10♠, J♣, K♠, A♥ (our sample), which deck (population) is this hand more likely to have come from?  How certain do you feel about your choice?

      b)  At the local game store you pick up two 6-sided dice.  One die is a "true" die, with which the chances of rolling a 1, 2, 3, 4, 5, or 6 are all equivalent.  The other die is a "loaded" die, that has been weighted so that the 1 happens very infrequently, the 6 occurs more frequently than usual, and the 2, 3, 4, & 5 occur at their normal rates.  The two dice look the same and you forget which is which.  So you decide to pick one of them and roll it 6 times (our sample).  Suppose that your sample roll is: 1, 1, 3, 2, 6, 2.  Which die do you think you selected, the "true" die or the "loaded" die? How certain do you feel about your choice?