Factorial ANOVA

Consider the following senario:

A researcher is interested in how reading to children affects those kids own reading ability. The researcher thinks that the age of the child being read to and how long each reading session is might be important variables. So the researcher designs the following experiment.

Three groups of children are selected: 3 yr olds, 8 yr olds, & 14 yr olds. Each group is read a Dr. Seuss story. Within each group, individuals are randomly assigned to one of three reading conditions. Reading sessions for group 1 only last 5 mins; 15 mins for group 2; and 30 mins for group 3. After two weeks the kids' reading ability is measured (with age appropriate standardized books).

		Reading session duration
		5 mins	15 mins	30 mins
Age	3 yrs
	8 yrs
	14 yrs

So we have not two samples, but 3 X 3 samples (that's 9). How do we analyze the data?

So far our Analysis of Variance (ANOVA) models have had only 1 factor (that's the "one-way" part). Often researchers aren't interested only in a single factor, but how multiple factors (independent variables) work together. The way the factors work together are called interaction effects.

In analysis of variance, a factor is an independent variable. A study that invloves only one independent variable is called a single-factor design. A study with more than one independent variable is called a factorial design.

The individual treatment conditions that make up a factor are called levels of the factor.

So the study described above is a factorial design, with two between groups factors, and each factor has 3 levels (sometimes described as a 3 by 3 between groups design).

For the most part we will focus on a 2-Factor between groups ANOVA, although there are many other designs that use the same basic underlying concepts.

Factorial - multiple factors

A factorial design is an experiment with two or more factors (independent variables).
• 2 x 4 design means two independent variables, one with 2 levels and one with 4 levels
• "condition" or "groups" is calculated by multiplying the levels, so a 2x4 design has 8 different conditions

Results
• Main effects
• Interaction effects

  * One should always consider the interaction effects before trying to interpret the main effects. Sometimes the interaction effects are the "cause" of the apparent main effects.

Partioning the variance of 2 factor between groups ANOVA

A = main effect of A

B = main effect of B

AB = interaction of A and B

There are lots (eight) of different potential outcomes:

1) No effects at all

2) A only

3) B only

4) AB only

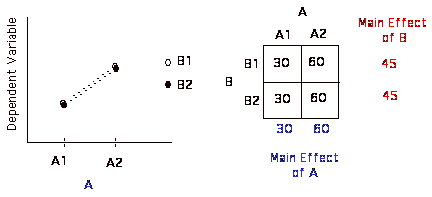
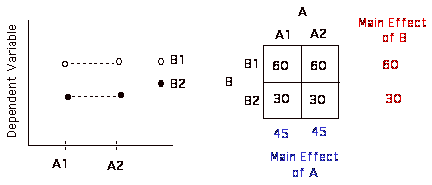
5) A & B

6) A & AB

7) B & AB

8) A & B & AB

Usually best way to look at your results are to look at a matrix that contains the cell means (the means of all of the separate conditions) and the marginal means (the means across the rows and down the columns).

Okay, now let's look at some of these possible patterns of results.

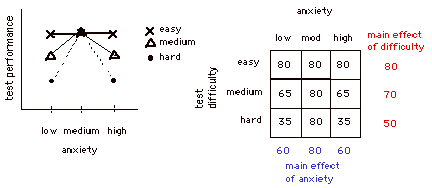
Let's look at a more complex design to see a more comlicated interaction. In this example there were two factors: anxiety (high med low) and test dificulty (hard medium easy). The dependent variable is test performance.  Let’s add another variable, test difficulty. 

Each of these different designs has advantages and disadvantages. 

 

Design	Advantages	Disadvantages
Two-level, single factor	It is efficient for determining if a variable has any effect	One cannot infer shape of functions
	Results are easy to interpret and analyze	Interpolation and extrapolation are dangerous
	It is adequate for some theory testing	Complex theories are difficult to test
	It is useful for applied comparisons
Multilevel experiment, single factor	One can infer shape of functions	It requires more participants or time
	Range of independent variable is less critical	Counterbalancing is more ponderous
		Statistics are more difficult
Factorial experiment	One can investigate interactions	Experiments become large as more factors are added
	Adding factors decreases variability, thus increasing statistical sensitivity	Statistics are more difficult to assess
	It increases generalizability without decreasing precision	Higher-order interactions are sometimes difficult to interpret
Converging-series experiments	They offer more flexibility than large factorial experiments	Interactions are difficult to assess
	They have built-in replications	Between-experiment comparisons are also between-subjects, with associated difficulties
		One must analyze prior experiment before doing the next

Partitioning of variance

Consider the data from a 2 X 3 between groups experimental design. There are 6 separate conditions, each condition has 5 subjects in it (so N = 30).

As was the case with the 1-way between groups ANOVA, we need to compute the sums, means, and Sums of Squares for each condition (this information is in blue) and for the overall data (grand in green). However, we've also got to compute the sums, means, and SS for each of the factors (A collapsed across B, in red & B collapsed across A, in purple).

Recall that our first stage of partitioning the variance is basically the same as we did for 1-way between groups ANOVA.

SS_total = S(X - grand mean)² = 340 (note: X refers to each of the thirty raw scores)
SS_{between treatments} = Sn(condition mean - grand mean)² = 5(5-4)² + 5(9-4)² + ... + 5(4-4)² = 220
SS_{within treatments} = SSS_{each condition} = 18 + 26 + 20 + 8 + 20 + 28 = 120


Now for the new Sums of Squares:

SS_{between A} = SS_A = = 15(6-4)² + 15(2-4)² = 60 + 60 = 120

(note: you could use instead)
SS_{between B} = SS_B = = 10(3-4)² + 10(5-4)² + 10(4-4)² = 10 + 10 + 0 = 20

SS_{interactionAxB} = SS_AxB = SS_{between treatments} - SS_A - SS_B = 220 - 120 - 20 = 80

df_total = N - 1 = 30 - 1 = 29

df_{between treatments} = total number of conditions - 1 = 6 - 1 = 5

df_within = N - total number of conditions = 30 - 6 = 24

df_A = K_A - 1 = 2 - 1 = 1

df_B = K_B - 1 = 3 - 1 = 2

df_AxB = df_{between treatments} - df_A - df_B = 5 - 1 - 2 = 2

For all of our F's (we'll have three for this example) we will use the MS_within as our denominator.

MS_within = SS_within/df_within = 120/24 = 5.0

MS_A = SS_A/df_A = 120/1 = 120.0

MS_B = SS_B/df_B = 20/2 = 10.0

MS_AxB = SS_AxB/df_AxB = 80/2 = 40.0

F_A = MS_A/MS_within = 120/5 = 24.0

F_B = MS_B/MS_within = 10/5 = 2.0

F_AxB = MS_AxB/MS_within = 40/5 = 8.0

Note: For each one you may need to look up a separate F_critical from the table because you may have different degrees of freedom for each F.

Assuming an alpha level of 0.05

F_crit for Main effect of A = F(1,24) = 4.26, 24.0 > 4.26 so we reject the H₀ for the main effect of A (so there is a difference between A1 and A2).

F_crit for Main effect of B = F(2,24) = 3.40, 2.0 < 3.40 so we fail to reject the H₀ for the main effect of B (so there are not differences between B1, B2, and B3).

F_crit for Interaction of AxB = F(2,24) = 3.40, 8.0 > 3.40 so we reject the H₀ for the interaction of A and B (so not all of the 6 conditions are equal).

Since this is a completely between groups Factorial design, we set it up like we did the independent samples t-test. The difference is that instead of having only one column for our Independent variable, here we have two columns, one for factor A and one for Factor B. Within each of these columns we specify what level each data point is in. Note that all of our raw scores from the dependent variable go into the same column.

The analysis for a completely between groups factorial ANOVA is found in the General Linear Model, Univariate submenu.

Now you need to specify what independent variables you want to enter into the factorial ANOVA analysis, and what dependent variable should be used.

Below is what your output should look like. The most relevant results are circled in red (I did this, SPSS doesn't circle any results for you)

Below is a set of data for you to practice with. The numbers are the raw numbers (so that means there are 5 subjects in each condition, 20 subjects total). I suggest that you try it by hand first, then use SPSS to check your answers.

		Factor A
		A1	A2
Factor B	B1	15 20 11 18 16	1 4 2 5 8
	B2	5 8 1 1 5	22 15 20 17 16

Click here to see the resulting ANOVA table