The Chi-Square Formula

Suppose that you have noticed that a lot of psychology majors are women with many fewer men. It could be that there are just more women enrolled in the university, and so you'd expect more women psych majors than men. Or, it could be that there is something about the psychology major that attracts women (or repels men?).
Both major and gender are categorical variables. Crosstabulation is a statistical technique used to display a breakdown of the data by these two variables (that is, it is a table that has displays the frequency of different majors broken down by gender).
The Pearson chi-square test essentially tells us whether the results of a crosstab are statistically significant. That is, are the two categorical variables independent (unrelated) of one another. So basically, the chi square test is a correlation test for categorical variables.
So for our example, the chi-square test will tell us whether there are more female psychology majors than you would expect by chance (based on total number of males and females and total number of people in different majors).
Example
Suppose that you are interested in whether there is a relationship between gender and educational level (undergraduate vs. graduate students) at ISU (year 2002). That is, are men and women equally likely to pursue a graduate education relative to an undergraduate education.
Setup our data in a "cross tabulation" of our two variables. The data are observed frequencies (fo).
| Student level | ||||
| Undergraduate | Graduate | |||
| Sex | Male | 7,715 | 938 | |
| Female | 10,780 | 1,625 | ||
The next step in the crosstabulation procedure is to compute the marginals for the rows and columns. This simply means add the frequencies across the rows and down the columns.
| Student level | |||||
| Undergraduate | Graduate | Row Marginals | |||
| Sex | Male | 7,715 | 938 | 8,653 | |
| Female | 10,780 | 1,625 | 12,405 | ||
| Column marginals | 18,495 | 2,563 | |||
So what can we tell from this table?
However this doesn't answer our question about whether women are more or less likely (i.e. that there is a relationship) to pursue graduate school than men. To find this out we need to do an inferential test, the Chi-square.
The Chi-Square Formula

Example
A manufacturer of watches takes a sample of 200 people. Each person is classified by age and watch type preference (digital vs. analog). The question: is there a relationship between age and watch preference?
Setup our data in a "cross tabulation" of our two variables. The data are observed frequencies (fo).
| Watch preference | ||||
| digital | analog | undecided | ||
| Age | under 30 | 90 | 40 | 10 |
| over 30 | 10 | 40 | 10 | |
Step 1: State the hypotheses and select an alpha level
| Watch preference | |||||
| digital | analog | undecided | |||
| Age | under 30 | 90 | 40 | 10 | 140 |
| over 30 | 10 | 40 | 10 | 60 | |
| 100 | 80 | 20 | |||
Part 2: Compute the expected frequencies

For people under 30
For people over 30
So let's enter the predicted (expected) values (in green) into our crosstabulation.
| Watch preference | |||||
| digital | analog | undecided | |||
| Age | under 30 | 90
70 |
40 56 |
10 14 |
140 |
| over 30 | 10 30 |
40 24 |
10 6 |
60 | |
| 100 | 80 | 20 | |||
Part 3: Compute the Chi-squared statistic


So then add them up


|
Choose Analyze, Descriptive Statistics, Crosstabs |
|
Select your categorical variables
Click on the Statistics button and then check the chi-square option.
|

|
Expected Counts
Multiply the marginal percentages together to get the expected percentage for that cell, then multiply by N to get expected counts Or, have SPSS compute them -- Choose Cells, Expected Counts
Residuals
Choose Cells, Unstandardized Residuals Standardized Residuals are distributed as z-scores (they were divided by the standard deviation of the residuals)
|

|
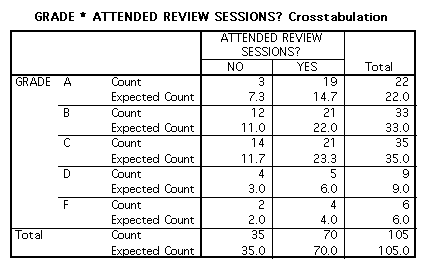
Output:Here is some sample output looking at a crosstab of final grade and review session attendance from the students.sav file.
|
|
|
Output shows Pearson chi-square and "Asymp. Sig." (significance level) for
the crosstab above. If "Asymp. Sig." is less than .05 then the residuals differ as a function of the independent variable
|

|
| Clustered bar charts are the most common way to present data from these crosstabulations (or as tables). You can get SPSS to plot your tables by clicking the Display Clustered Bar Charts box on the main cross tabs window. | 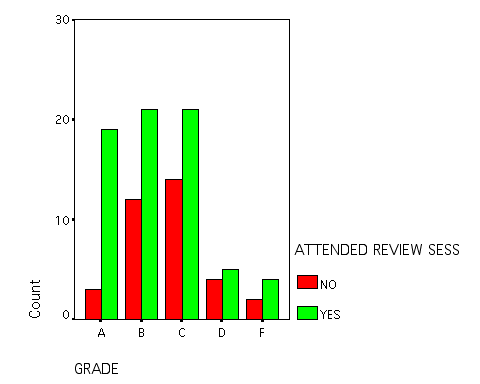
|
| Aggression content | ||||
| low | medium | high | ||
| Gender | Female | 18 | 4 | 2 |
| male | 4 | 17 | 15 | |
2) Suppose that you're interested in whether there is a relationship between sex and membership in an after-school club (in high school students). So you randomly selected 30 students from a local high school and recorded their sex and whether or not they were members of an after-school club. Create a crosstabulation for the following data.
|
|
3) Using SPSS, compute the marginals and expected values and chi-squre for the data in (2).
For the following two questions download the file students.sav.
4) Were juniors and seniors more likely than freshmen and sophomores to
attend the review sessions? Provide a bar chart showing the breakdown.
Assuming an a = 0.05, test whether these
variables are independent. Remember to state your hypotheses.
5) Were men more likely than women to do an extra credit assignment?
Report the number of people who did and didn't do the extra credit project
broken down by gender. Assuming an a = 0.05,
test whether gender and extra credit participation are independent.
Remember to state your hypotheses.