Last time we introduced the General Linerar Model for Bivariate Regression (regression with only two variables). Now we will learn about regression with more than two variables (multiple regression). That is, we'll still be predicting one variable (Y), but now we'll use several explanatory variables (e.g., X1, X2, & X3).
For bivariate regression we stated the model as:
For multiple regression the FIT portion of the model gets more parts. For each additional explanatory variable we add a new Beta (the Beta's are often called parameters).
Note: now B1 is no longer interpreted simply as the slope of the line. Rather, it is a measure of how much the its associated explanatory variable (X1) contributes to the model predicting the response variable (Y).
With multiple regression, it is typical to examine several models to see
which set of variables offer the best prediction. Along with each model
may be several hypothesis tests. Basically each model will have an
R2, an ANOVA result which tests the overall Model, and a t-test
result for each explanatory variable (and the intercept, although this is
still not usually of theoretical interest).
Squared multiple correlation (R2) is still a measure of how
much of the variance in the response variable (Y) can be accounted for by
the explanatory variables (now, X1, X2, ...,
Xp). Typically it'll be the first result that you examine when
comparing different models. Generally, the higher the R2 the
better the model. This gets balanced in practice with a parsimony
principle which states that the simplier the model (the fewer the
explanatory variables) the better. So when comparing models, these two
factors may trade-off and the researcher needs to decide how much of a
change in the R2 is needed to pick a more complex model over a
simple one.
The computation of R2 is:
In addtion to the descriptive statistic R2, there is a statistical
test of the overall model.
The null hypothesis that the ANOVA is testing is that all of the betas
(except for the intercept) are equal to zero.
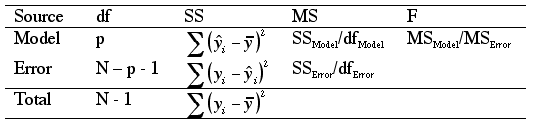
Here are the formulas that go into the different components of the ANOVA.
For this class you won't have to do any of these compuations by hand (so
the table below is just for those who want to know more).
In addition to the overall ANOVA result, the statistical analysis of each
model will include individual t-tests for each of the Betas (there will be
one for each explanatory variable in the model). Unlike in bivariate
regression (with only one explanatory variable, X) the Beta is no longer
simply the slope of a line. Instead, the Beta should be thought of as a
weighting of how much its paired explanatory variable contributes to the
overall model. That is, it tells us whether the explanatory variable
actually does any "explaining."
Hypothesis testing with mulitple regression
H0: B1 =
B2 = ... =
Bp = 0
The alternative is that at least one beta is not equal to 0.
Multiple regression analyses in SPSS use essentially the same procedures that we used for Bivariate regression, except now we will add more than one independent variable.
To review:
To follow along the example in SPSS, you may download the height.sav datafile.
Let's start a simple bivariate regression to predict height based on a person's average calcium intake in their first 5 years.
The output looks like this:
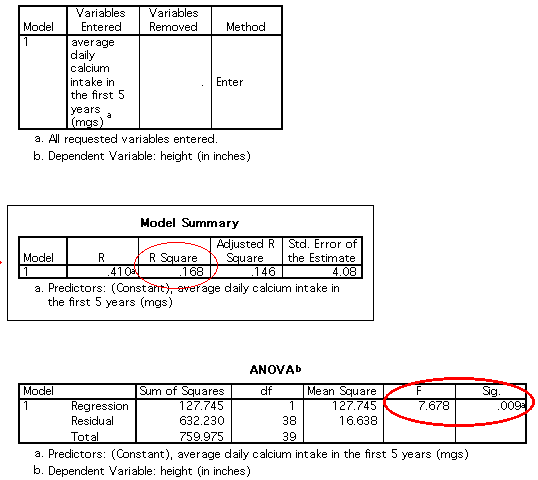
|
Rather than always present all of this output, I'll just report a summary of the results for different models. So for the output above, the summary would be:
Let's compare this model against another bivariate model. Let's predict height with weight. The summary of the results are as follows:
Compare the two models. Both are significant (both have significant ANOVAs). That means that both weight and calcium intake can predict a significant portion of the variability in height. The first model (calcium) accounts for 16.8% of the variance. The second model (weight) accounts for 63.1% of the variance in height. This suggests that weight is a better predictor of height than calcium intake in the first five years.
Now let's look at a multiple regression model that predicts height with both weight and calcium intake. The model summary is:
There are several things to note.
The bivariate model has these results:
This model accounts for 64.1% of the variance in height. Relative to our other models, that seems like a lot. So let's add parent's average height to our Model 3 (calcium and weight) and see if we can account for (nearly) the rest of the variance.
Model 5 looks great.
This model accounts for just as much variability in height as the previous model (7). Which is considered the "better" model? If selecting between two models which account for about the same amount of variance, the model that contains the fewest explanatory variables (the simpliest) is generally considered the best model.
Advanced topic: There are a number of different methods of entering
variables into the regression equation. The default is to enter them as
entered into SPSS. To use other methods, you use the menu box labeledMethod. This allows you five
different methods of entering variables into the regression equation. *
on the down arrow to make them appear.
Generally the best way to enter your variables is to enter them into the model in an order that is guided by your theory. That is, your theory should make some claims about what variables should be important and what variables should not be. |
To follow along the example in SPSS, you may download the CSDATA.sav
datafile.
This is the data set that your textbook uses as the case study in chapter
11 (multiple regression). The suggested questions below are taken
(roughly) from the chapter to help facilitate the connection between what
you do in class with SPSS and what the book says (note: the book uses a
different statistical package, so the output in the book is in a different
format than your SPSS output will be).
The CSDATA data set has the following variables:
A good first step of most analyses is to compute the descriptive
statistics of your data.
1) Using SPSS, compute the mean and standard deviations of the continuous
variables (GPA, SATM, SATV, HSM, HSS, HSE).
2) Compute the correlations between the continuous variables (you can do
this all at once in one big correlation matrix).
Suppose that your theory is that High School grades should be better
predictors (explanatory variables) of University GPA than standardized
tests (SAT scores).
So you may want to start by comparing two multiple regression models.
3) Using SPSS compute the regression analysis for Model 1
b) Which explanatory variables (if any) are significant predictors? Which
do not explain any of the variance?
c) How might you develop a new "better" model based on Model 1?
4) Using SPSS compute the regression analysis for Model 2
b) Which explanatory variables (if any) are significant predictors? Which
do not explain any of the variance?
c) How might you develop a new "better" model based on Model 2?
5) Compare Model 1 and Model 2. Which does a better job predicting
University GPA?
6) Given the results of Model 1 and Model 2 how might you improve your
prediction of University GPA (what other Model(s) might you try)?
7) In your opinion, is the Model which includes all of the variables (HSM,
HSS, HSE, SATM, SATV) "better" than Model 1? Is it better than a Model
that only includes HSM?
a) Is the model significant? How much of the variance does it account for?
a) Is the model significant? How much of the variance does it account for?