A First Course for Students of Psychology and Education, 4th Edition. New York: West Publishing.
Descriptive statistics, like the mean and standard deviation, describe distributions by summarizing the center (central tendency) and spread (variability). While this isn't evey detail about a distribution, it does give us a pretty good picture of what the distribution looks like.
-
for most bell-shaped curves (e.g., symmetric and unimodal), the mean should be at
the mid-point and the standard deviation should be somewhere half-way
between the mean and the most extreme values.
Our goal is to be able to find our raw scores within the distribution, and to be able to describe where it falls.
A good point of reference is the mean (since it is usually easy to find). So a natural choice for describing the location of a data point would be the deviation score (x - m) or (x - 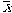 ).
).
If we are only concerned about a single distribution, then this seems to be pretty easy to do. But, if we want to compare two scores from two distributions, then the situation gets much harder.
Consider the following situation. You take the ACT test and the SAT test. You get a 26 on the ACT and a 620 on the SAT. The college that you apply to only needs one score. Which do you want to send them (that is, which score is better, 26 or 620?).
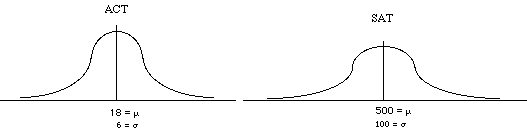
It is hard to do a direct comparison here because the two distributions have different properties: different means, and different variabilities.
How might we go about it? 1) look at the distribution graphs, locate the scores and compare -- still hard to tell 2) think about cumulative percentiles and percentile ranks -- this will work 3) try and take the deviations and standard deviations into account
- e.g., ACT mean = 18, SD = 6, deviation = 26 - 18 = 8
so an 8 is 1.33 SD above the mean (8 / 6)
SAT mean = 500, SD = 100, deviation = 620-500=120
so a 620 is 1.2 SD above the mean (120 / 100)
- so the ACT score is better than the SAT score
The comparison that we just did is what z-scores are all about.
So to be able to make a comparison, one approach would be to transform both distributions into a standardized distribution.
-
A standardized distribution is composed of transformed scores that result in
predetermined values for m and s, regardless of their values for the raw
score distribution. Standardized distributions are used to make dissimilar
distributions comparable.
-
A standard score is a transformed score that provides information about its
location in a distribution. A z-score is an example of a standard score.
A z-score specifies the precise location of each X value within a distribution. The sign of the z-score (+ or -) signifies whether the score is above the mean or below the mean. The numerical value of the z-score specifies the distance from the mean by counting the number of standard deviations between X and m.
For z-scores the mean of the distribution is always 0 and the standard deviation is always 1.

So what this means is that a z-score of 1, means that the data point is exactly 1 standard deviation away from the mean. If it is a positive 1, it means that the score is 1 standard deviation above the mean, if it is a negative 1, then it means that the score is 1 standard deviation below the mean.
So how do we do this transformation?
population |
sample |
||
Z = deviation = standard deviation |
 |
= |  |
Now let's return to our ACT and SAT example. Notice what we did there, we subtracted the the distribution means from the scores, and then we divided by their standard deviations. In otherwords what we did was transform them into Z-scores. And then we made the comparisons based on those Z-scores.
We can transform any & all observations or values from a distribution to a z-score if we know either the m & s, or the 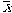 & s.
& s.
We can also transform a z-score back into a raw score if we know the mean and standard deviation information of the original distribution. Let's look at the algebra.
So suppose that you know somebody else who said that they go 2 SD above the mean on the SAT. How would we go about figuring out their score?
-
2 SD above = Z of 2.0
we know that the mean of SAT = 500, and the SD = 100, so we just plug in the numbers
-
X = (Z)( s) + m = (2)(100) + 500 = 200 + 500 = 700
Properties of the z-score distribution.
Shape - the shape of the z-score distribution will be exactly the same as the original distribution of raw scores. Every score stays in the exact same position relative to every other score in the distribution.
Mean - when raw scores are transformed into z-scores, the mean will always = 0.
Z = (X - m) s |
m = 100; s = 10 (100 - 100) / 10 = 0 m = 200; s = 10 (200 - 200) / 10 = 0 m = 100; s = 20 (100 - 100) / 20 = 0 |
The standard deviation - when any distribution of raw scores is transformed into z-scores the standard deviation will always = 1.
Z = (X - m) s |
m = 100; s = 10 (110 - 100) / 10 = 1 m = 200; s = 10 (210 - 200) / 10 = 1 m = 100; s = 20 (120 - 100) / 20 = 1 |
-
In other words:
-
The transformation procedure really is just a way of relabeling the axis of
the distribution. So imagine that you leave the curve alone, but just draw
new labels on the X-axis -- centering it on 0 and making each SD interval
equal to 1.
EXAMPLE: Heights and weights of the men in stats 240 sec 04 (who responded)
person height weight |
height2 weight2 |
| height m = 710 / 10 = 71.0 SS = 50486 - (710)2 / 10 = 76.0 s = 2.8 |
weight m = 2000 / 10 = 200.0 SS = 408346 - (2000)2 / 10 = 8346.0 s = 28.9 |
 |
 |
| Z = (X - m)
s
Z1 = (66 - 71)/2.8 = -1.8 Z2 = (71 - 71)/2.8 = 0 Z3 = (74 - 71)/2.8 = 1.1 Z4 = (69 - 71)/2.8 = -0.7 Z5 = (70 - 71)/2.8 = -0.4 Z6 = (74 - 71)/2.8 = 1.1 Z7 = (73 - 71)/2.8 = 0.7 Z8 = (69 - 71)/2.8 = -0.7 Z9 = (69 - 71)/2.8 = -0.7 Z10 = (75 - 71)/2.8 = 1.4 |
Z = (X - m)
s
Z1 = (203 - 200)/28.9 = 0.1 Z2 = (174 - 200)/28.9 = -0.9 Z3 = (223 - 200)/28.9 = 0.8 Z4 = (175 - 200)/28.9 = -0.9 Z5 = (144 - 200)/28.9 = -1.9 Z6 = (219 - 200)/28.9 = 0.7 Z7 = (184 - 200)/28.9 = -0.6 Z8 = (237 - 200)/28.9 = 1.3 Z9 = (204 - 200)/28.9 = 0.1 Z10 = (237 - 200)/28.9 = 1.3 |
| notice that the sums of the z-scores = 0 so the mean of the z-scores = 0 | the standard deviations = 1 (a little off here due to round off) |
 |
 |
So now we can compare for each person where they are in the two distributions and how their weights and heights compare to one another ("too tall for my weight" or "just right", etc.)
Person #4:
- -.7 stdev below height mean (so shorter than the mean)
-.9 stdev below weight mean (so lighter than the mean)
on the other hand:
Person # 8:
- -.7 stdev below height mean, but
1.3 stdev above the weight mean
US male height mean is around 5'9" (69 inches), stdev ??? US male weight mean is around ???, stdev ???
So if we wanted to know how our mean corresponds with the US or even the world-wide population of males, how would we go about it?
Well, the numbers that we have are descriptive statistics, to go from samples to populations we'll need to start thinking about inferential statistics.
We'll start getting there next time, in chapter 6, when we begin our discussion of probabilities. Remember that what we'll be doing is using our sample statistics to make estimates of population parameters. These estimates/relationships are described in terms of probabilities.